Functional Commitments for Arbitrary Circuits of Bounded Sizes

任意有界电路的函数承诺方案

Jinrui Sha, Shengli Liu*,Shuai Han*

研究目标

近年来，关于函数承诺的研究取得了许多进展。衡量函数承诺的一个重要的标准是函数到目前为止，现有的所有函数承诺方案所支持的最大函数集合是深度有界的布尔电路。然而，这些函数承诺方案很难扩展到支持任意电路。这是因为这些方案都利用了同态编码技术来处理电路。然而，同态计算中的噪声积累会随着电路深度的增长指数级别增长。所以当深度较大时，这些函数承诺方案的安全性就无法得到保证。基于这样的原因，我们希望在格上构造支持任意有界电路的函数承诺方案。

关键问题

是否基于可伪造的后量子假设，在格上构造支持任意（多项式大小）电路的函数承诺方案？

研究内容

本工作中，我们我们引入了一个通用框架，给出了满足任意有界电路的函数承诺的形式化定义和安全性定义。也在格上构建了一个任意有界电路的函数承诺方案，支持私密展开性和目标绑定性。同时我们的函数承诺方案具有简洁的承诺和准简洁的证明。

本工作还采用了非交互式的GKR协议，将验证算法的部分工作量外包给了计算算法，进一步降低验证复杂度，构建了支持快速验证的任意有界电路函数承诺方案，并同样支持私密展开性和目标绑定性，具有简洁的承诺和准简洁的证明。

技术路线

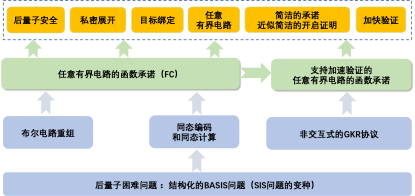
本工作我们使用了同态编码和同态计算技术。与其他工作中，对布尔电路直接进行同态编码技术不同的是，我们将原电路进行拆解，处理电路中的每个门，然后将处理后的门重新组装成一个深度很低的新的扁平电路，在使用同态编码和同态计算技术处理。对于电路中每条线的值，利用公共引用字串中的公开矩阵和承诺算法的输出可以得到每条线的值乘Gadget陷门。之后利用同态编码和同态计算，可以在验证算法中，利用函数在输入点的值来进行验证。我们的方案实现了目前第一个不限制电路层数，可以支持任意有界电路函数承诺方案。

研究意义

本工作中，我们引入了一个通用框架，给出了满足任意有界电路的函数承诺的形式化定义和安全性定义，也基于后量子的同态编码和同态计算技术，在格上构建了一个任意有界电路的函数承诺方案。目前其他满足后量子安全的函数承诺方案，对函数的最低要求需要对函数转化的布尔电路的深度进行限制，这是因为同态计算中的噪音是指数级别累计的。本方案则将原电路进行拆解，处理电路中的每个门，然后将处理后的门重新组装成一个深度很低的新的扁平电路，实现了目前第一个不限制电路层数，可以支持任意有界电路函数承诺方案。我们任意有界电路的函数承诺方案支持私密展开性，在结构化的BASIS假设下实现了目标绑定性。同时我们的函数承诺方案具有简洁的承诺和准简洁的证明。

我们还采用了非交互式的GKR协议，将验证算法的部分工作量外包给了计算算法，进一步降低了验证复杂度，构建了支持快速验证的任意有界电路函数承诺方案，该方案依然支持私密展开性、目标绑定行，并具有简洁的承诺和准简洁的证明。