Reusable Fuzzy Extractor from Isogeny

基于同源的可重用模糊提取器

Yu Zhou, Shengli Liu*, Shuai Han

研究目标

密钥是密码系统中最重要的部分之一，如何获得高质量的密钥是一个备受关注的问题。现实中有许多常见的高熵噪声源（例如生物信息等），但是从中提取出的密钥会受到噪声的影响从而难以使用。模糊提取器正是一种为了解决：“如何从随机的高熵噪声源中提取出可复现的高质量密钥”这个问题的密码工具。但是，许多模糊提取器方案在对同一个噪声源进行多次提取时，可能会因泄漏过多关于源的信息而丧失安全性。为了解决这一问题，密码学家提出了可重用模糊提取器（rFE）的概念。rFE保证了对同一噪声源进行多次提取的结果依然是（伪）随机的。同时，为了使rFE具有更强的实用性，往往会尝试让其具备线性纠错能力。

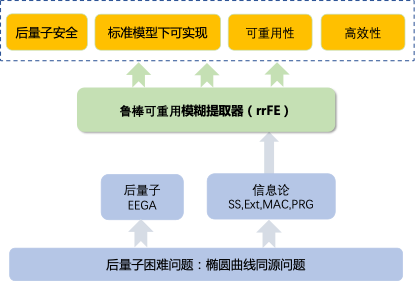
到目前为止，已经出现了众多的rFE方案。其中，具备后量子安全的方案数量较少，且都是基于LWE假设或LPN假设实现的。为了增加后量子安全rFE方案的多样性，我们将目光放在了椭圆曲线同源（简称同源）假设上。相较于其他后量子困难假设，基于同源假设所构造的方案往往具有更短的公钥和密文尺寸，从而有着更低的通信开销。

因此，我们的研究目标就是在椭圆曲线同源假设下设计具有线性纠错能力的后量子安全的rFE方案。

关键问题

我们注意到，基于同源假设的密码系统有时与基于离散对数等问题的系统较为相似。因此，我们尝试将同源假设融入到之前到rFE框架中。我们发现，基于DDH假设的方案在形式上与椭圆曲线同源较为相似，故试图构造类似的方案。然而DDH假设在椭圆曲线同源的设置下并不成立，因此，如何证明基于同源的rFE方案的安全性就成为一个最重要的问题。

研究内容

我们围绕：“如何在标准模型下基于椭圆曲线同源假设构造具有线性纠错能力的可重用模糊提取器”这一主题展开研究。

技术路线

我们利用有效群作用（EGA）、安全梗概（SS）和提取器（Ext）设计出了一个rFE的方案。EGA是将同源问题和传统的离散对数等问题整合起来的一个抽象概念，并且可以基于同源假设来具体实现。我们发现，EGA拥有一个重要的安全性，称为弱伪随机性。因此，基于同源的EGA就拥有弱伪随机性。同时，虽然DDH假设在同源上不成立，但DDH假设的困难性却可以归约到弱伪随机性上。因此，我们就为新方案找到了一个底层的安全性，并且成功地证明了我们基于同源的rFE方案的可重用性可以归约到底层基于同源的EGA的弱伪随机性上。此外，因为我们的方案对于纠错的部分没有额外的限制，所以基于同源的rFE方案可以实现线性的纠错率。

研究意义

我们的基于椭圆曲线同源假设实现的rFE方案，是首个支持基于椭圆曲线同源假设的rFE方案，并且支持线性纠错。此外，我们的方案计算非常简单高效，仅仅需要处理一次群作用。在仿真实验中，rFE调用一次生成算法仅需几百毫秒，有着良好的实用价值。我们的成果被会议ProvSec录用。