Home
Research
Teaching
Publications
Software

Yi Hong

Shanghai Jiao Tong University

I am interested in theory development and applications to medical problems as well as to general computer vision problems. Currently, my research focuses on deep learning, spatiotemporal image and shape analysis, statistical estimation and testing on mainfolds, and atlas-building. In particular, my research interests lie in

  • Deep segmentation networks for medical images,

  • Deep image regression for longitudinal data,

  • Diagnostic classification network for identifying lung nodules,

  • Parametric regression on the Grassmannian,

  • Estimating spatiotemporal changes from image data,

  • Detecting and locating shape differences between populations,

  • Statistical testing for longitudinal data,

  • Statistical atlas with application to upper airway obstruction.

I am also interested in physically-based modeling, simulation and animation in computer graphics. I worked on physically-based fire simulation.

Deep Segmentation Networks for Medical Images

Image segmentation is a fundamental task in image understanding, which distinguishes regions of interest (ROI) from image background for further analysis. Deep neural networks have been widely used in medical image segmentation with promising segmentation performance. However, there exist several challenges in existing methods, e.g., how to obtain robust segmentation with limited labeled data and how to achieve accurate and computationally efficient segmentation for 3D high-dimensional images.

To robustly segment ROI from pathological images with only normal control images as input, we propose a complementary segmentation network (CompNet) that fully leverages the information within the ROI and also the complementary information outside the ROI. In this way, We use the normal control images to train the network not just what is the ROI but also what is not the ROI, resulting in a more robust solution even without the need of pathological images for training. We evaluate our CompNet on the brain extraction task using the OASIS dataset, which shows over 97% Dice score for skull stripping from both non-pathological and synthetic pathological image scans. In addition, we use both 2D and 3D CompNets in a cascaded system to segment hepatic lesions effectively. Our 2D CompNets operate on a slice-by-slice basis in the axial orientation to segment liver and large liver lesions; while we use a 3D CompNet to detect small lesions that are often missed in a 2D segmentation design. This hybrid design balances the accuracy and efficiency in the 3D image segmentation.

Another piece of work we develop to achieve high segmentation accuracy with low computational cost is a multi-dimensional attention network (MDA-Net), which efficiently integrates slice-wise, spatial, and channel-wise attention into a U-Net based network. We evaluate our MDA-Net on the MICCAI iSeg and IBSR datasets, and the experimental results demonstrate consistent improvements over existing methods.

Deep Image Regression for Longitudinal Data

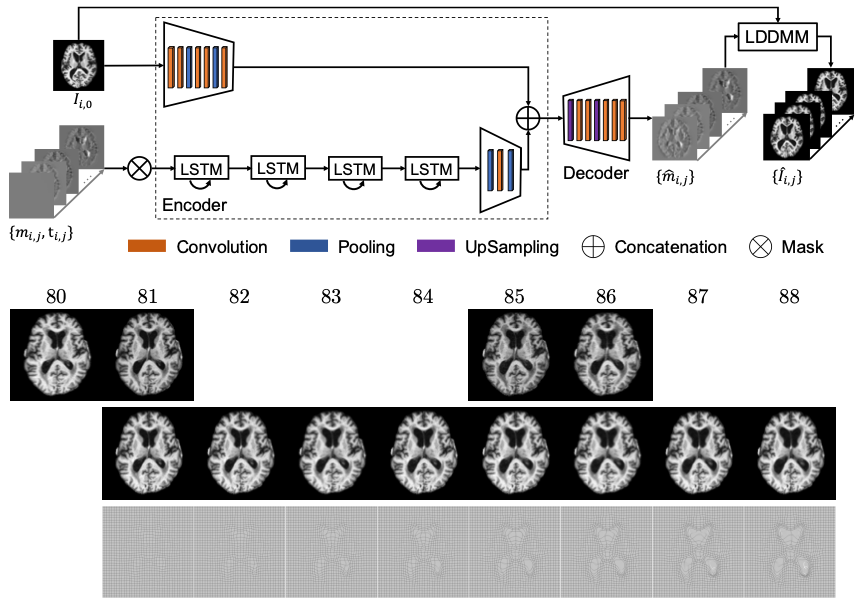Longitudinal images are increasingly available for studying brain development and degeneration, disease progression, and aging problems. To predict follow-up image scans for a specific subject based on a population of longitudinal images, we often summarize the time-varying changes of a population and then parallel transport the group trajectory to the target subject. However, parallel transport techniques are non-trivial. Another choice is to directly predcting image scans using deep neural network, which results low-resolution or blurring image predictions. Therefore, we propose a predictive regression model for longitudinal images with missing data based on large deformation diffeomorphic metric mapping (LDDMM) and deep neural networks. Instead of directly predicting image scans, our model predicts a vector momentum sequence associated with a baseline image. This momentum sequence parameterizes the original image sequence in the LDDMM framework and lies in the tangent space of the baseline image, which is Euclidean. A recurrent network with long term-short memory (LSTM) units encodes the timevarying changes in the vector-momentum sequence, and a convolutional neural network (CNN) encodes the baseline image of the vector momenta. Features extracted by the LSTM and CNN are fed into a decoder network to reconstruct the vector momentum sequence, which is used for the image sequence prediction by deforming the baseline image with LDDMM shooting. To handle the missing images at some time points, we adopt a binary mask to ignore their reconstructions in the loss calculation.

Diagnostic Classification Network for Identifying Lung Nodules

Lung cancer is the leading cause of cancer-related death worldwide. Early diagnosis of pulmonary nodules in Computed Tomography (CT) chest scans provides an opportunity for designing effective treatment and making financial and care plans. We consider the problem of diagnostic classification between benign and malignant lung nodules in CT images, which aims to learn a direct mapping from 3D images to class labels. To achieve this goal, four two-pathway Convolutional Neural Networks (CNN) are proposed, including a basic 3D CNN, a novel multi-output network, a 3D DenseNet, and an augmented 3D DenseNet with multi-outputs. These four networks are evaluated on the public LIDC-IDRI dataset and outperform most existing methods. In particular, the 3D multi-output DenseNet (MoDenseNet) achieves the state-of-the-art classification accuracy on the task of end-to-end lung nodule diagnosis. In addition, the networks pretrained on the LIDC-IDRI dataset can be further extended to handle smaller datasets using transfer learning. This is demonstrated on our dataset with encouraging prediction accuracy in lung nodule classification.

Parametric Regression on the Grassmannian

Many data objects in computer vision and medical problems admit a subspace representation. Examples include feature sets obtained after dimensionality reduction via principal component analysis (PCA), observability matrix representations of linear dynamical systems, or landmark-based representations of shapes. Such data objects can be interpreted as points on the Grassmannian \(\mathcal{G}(p, n)\), the manifold of \(p\)-dimensional linear subspaces of \(\mathbb{R}^n\). To address the problem of fitting parametric curves on the Grassmannian, we start from the energy minimization formulation by generalizing linear least-squares in Euclidean space, resulting in a geodesic model which is further extended to a “time-warped” variant and cubic splines. This is achieved by using optimal-control, which not only allows to easily generalize regression to manifolds but also to define more complex parametric models on these manifolds.

Take fitting straight lines in \(\mathbb{R}^n\) for example. Such a line can be defined as an acceleration-free curve and at each time-point it can be represented by two states, its position and velocity. The states at time \(0\) are referred to the initial conditions. By introducing time-dependent Lagrangian multipliers for each state, we can derive an adjoint system, which is integrated backward to evaluate gradients for updating the initial conditions. This optimal-control perspective constitutes a general method for estimating first-order curves, which allows to generalize the notion of straight lines to manifolds, i.e., geodesics. To increase the flexibility of fitting curves, the idea of time-warped regression is to use a simple model to warp the time-points, or more generally the independent variable, when computing the data matching errors. As a result, a basic geodesic model may be sufficient to fit the data in the warped domain. To further increase the flexibility of a regression model, cubic splines are another commonly used technique. To enable cubic spline regression, we add an external force and represent an acceleration-controlled curve using a dynamic system with three states. Similar to geodesic regression, a shooting solution can be achieved for cubic-spline regression on the Grassmannian via optimal-control.

Now, we have three regression models, i.e., the basic geodesic regression, a time-warped variant, and a cubic-spline version. Which one is suitable for the data? A recent model criticism approach allows us to check if a model fits and if the underlying model assumptions are justified by the observed data. We investigate and extend this approach to evaluate our three regression models on the Grassmannian. In particular, we extend the approach by (1) providing a strategy to generate Gaussian-distributed samples with a specific variance on the underlying manifold, and (2) incorporating existing kernels into the two-sample testing strategy used for model criticism.

Estimating Spatiotemporal Changes from Image Data

In medical research, image time-series from one subject or a population are collected to study aging, disease progression, and brain development. To capture shape and appearance changes in these spatiotemporal data, regression analysis is popular due to its power of modeling the relationship between data objects and associated descriptive variables, e.g., age. When building regression models for image time-series, one challenge is capturing spatial and intensity changes simultaneously. Such changes occur in MRI studies, e.g., the developing brain due to myelination.

Image metamorphosis aims to jointly account for spatial and intensity changes for two images. It allows exact matching of a target image by an intensity-adjusted image warped from a source image. This is achieved by adding a control variable, which serves as a “source” term and smoothly adjusts image intensities along streamlines. We proposed a shooting solution for image metamorphosis through optimal-control approaches, which is called shooting metamorphosis. It turns out the introduced control variable can be well represented by the state for metamorphosis, i.e., the initial momentum, which is identical to the state for the LDDMM (large displacement diffeomorphic metric mapping) registration.

Similar to shooting metamorphosis, a metamorphic regression formulation can be achieved through estimating a regressed geodesic (under the geodesic equations for metamorphosis) which fits a set of images instead of just two images. This is achieved by minimizing the sum of squared geodesic distances between image measurements and their corresponding estimated images on the regressed geodesic, plus a regularity term that controls the smoothness of the regressed curve. To simplify the solution of metamorphic geodesic regression, the distance between two images is approximated with respect to a base image, which results in an approximate solution with an appropriate averaging of the initial momenta of independent pair-wise shooting metamorphosis. This idea enables to jointly and efficiently captures spatial deformations and intensity changes in image time-series.

Detecting and Locating Shape Differences Between Populations

Shape analysis approaches have been proposed to assess object properties beyond global volume and to characterize shape variations across subjects and between subject populations. The methods can be roughly subdivided into two categories: methods for global analysis, i.e., detecting if population shape differences exist, and methods for local analysis, i.e., locating these differences with point-to-point correspondence between shapes. Most existing methods are based on the classical point distribution model (PDM), which assumes a Gaussian distribution of the points around the mean shape. We aim to develop a new approach that is free from strong distributional assumptions, while detecting potential global and local differences between shape populations without an explicit computation of dense correspondences.

To achieve this goal, we propose to perform shape analysis based on the ordering of shapes using band-depth, which non-parametrically defines a global depth for a shape with respect to a population. Based on the depth and the ordering of a shape population, statistical tests are defined to globally separate control and disease groups using global analysis with a scalar value (depth) for each shape. Statistical difference for global analysis results can be established through permutation testing. Equivalently, local shape differences can be detected using local analysis with a corresponding local permutation test, resulting in \(p\)-values on the surface of a shape to establish local shape differences between populations. The directionality of the shape differences (inflation versus deflation) can also be determined.

Statistical Testing for Longitudinal data

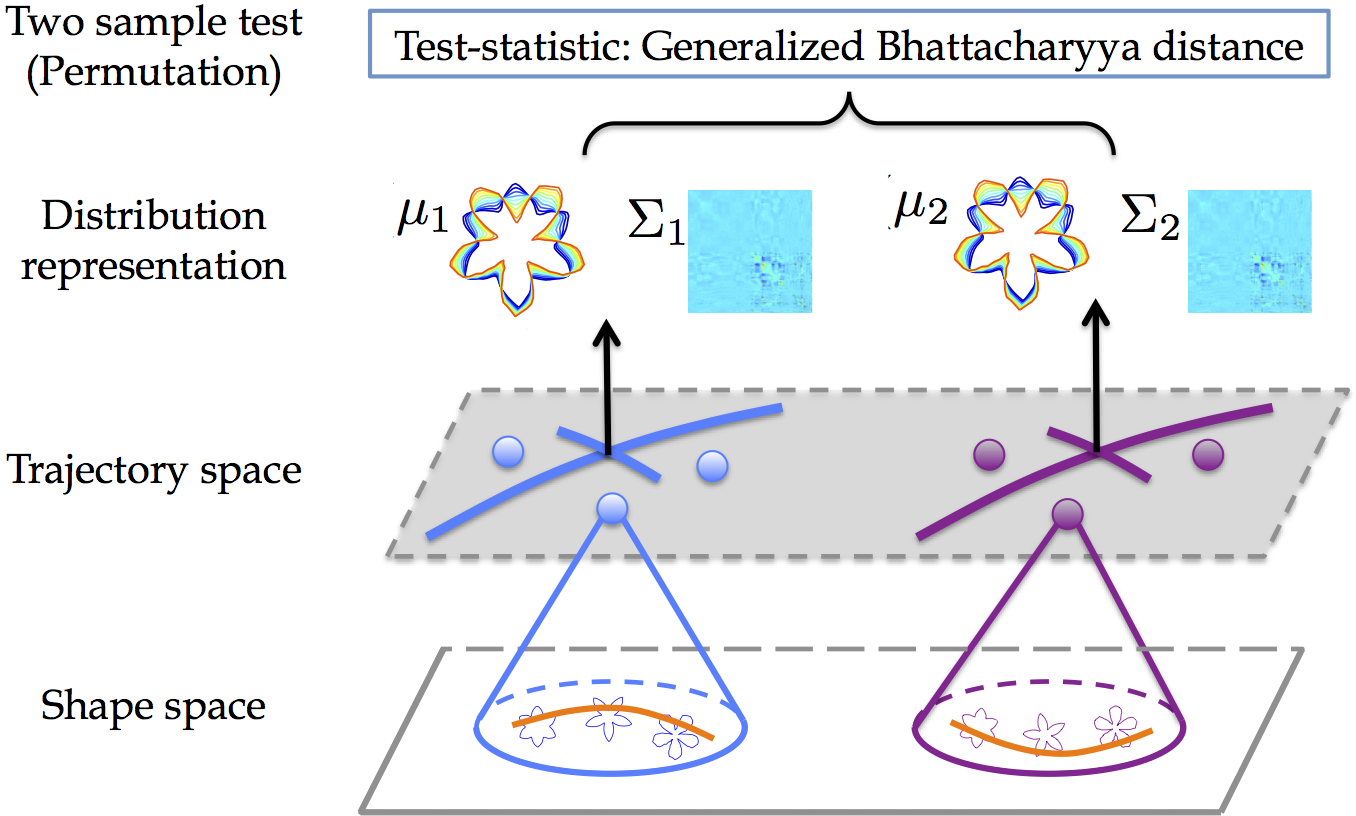Longitudinal data designs frequently arise in medical research that involves repeated measurements during follow-up studies. For example, longitudinal studies in new-borns and young children use imaging at multiple follow-up visits to understand the process of early brain development. Recent methods for analyzing longitudinal, manifold-valued data allow for the estimation of trajectories, i.e., a smooth path estimated from the longitudinal data of subjects. Building upon these methods, approaches that compute averages of trajectories has been proposed; while they only capture limited information of the data distribution. Our goal is to develop an approach that leverages second-order statistics of shape trajectories for testing group differences. This higher-order description would be useful for a more comprehensive description of the underlying distributions. It would even benefit for designing test-statistics that go beyond a simple comparison of means, potentially resulting in strong statistical testing power.

In particular, we propose a generalization of principal geodesic analysis (PGA) to the tangent bundle of a shape space, where longitudinal data of a subject is represented as a point using initial conditions of a trajectory, and estimate both variance and principal directions of shape trajectories. We then introduce a generalization of the Bhattacharyya distance. It accounts for both mean and variance differences in trajectory distribution, which enables the assessment of statistical differences between groups of trajectories.

Statistical Atlas with Application to Upper Airway Obstruction

Abnormalities of the upper airway in infants and children may lead to life threatening respiratory difficulties, poor growth, delay in speech development and long term morbidity. Methods of evaluating and determining optimal management for upper airway anomalies would be of tremendous benefit for improved clinical care and outcomes. To track and measure these anomalies, a pediatric airway atlas built from normal subjects is needed as a reference. Such an atlas would generally provide a domain for understanding airway growth patterns; it could also be customized to specific patients to capture airway stenoses. We propose a method to construct a pediatric airway atlas based on normal subjects. This method makes use of a simplified airway model and allows age-adapted atlas computations through kernel regression combined with the computation of statistical characterization of the population data using the weighted functional boxplot. This allows the generalization of concepts such as the median, percentiles, or outliers to spaces of data objects, not only functions, e.g., the pediatric airway application, but also shapes and images, e.g., corpos callosum shapes and its binary images.

Physically-Based Fire Simulation

Natural phenomena simulation, e.g., fire, is commonly used in entertainment, video games, and fire prevention training. Physically-based modeling and animation allows to simulate real fire effect, while it has the challenge of controlling the behaviors of the simulated fire due to the non-linear properties of the underlying physical model. Our goal is to provide users the power of high-level control of fire while keeping the benefits from the physical model, resulting in a detail-free user interface to make desirable flame effects. The high-level control, for example, geometric constraints, e.g., mesh animation, and evolving rules, e.g., speed, are automatically converted and included in a control blue core (CBC), which is further leveraged by a defined L-Speed function and serves as the guidance of the large-scale motion of the fire. At the same time, the fire details are captured by the underlying physical model. To solve the model under the constraints of a sequence of evolving CBCs, we develop a modified closest-point model (MCPM) for dynamic constraints, since the original approach is limited to the statistic constraints.